How to reduce package thermal resistance?
Thermal management is one of the most important and challenging issues in electronics packaging. It’s a difficult problem with no perfect solution, yet it is still an area where advances can be made. Thermal resistance measurements are often conducted on packages to evaluate the effectiveness of different approaches to thermal management as well as compare competing solutions from various suppliers. In this article, we will discuss how to reduce package thermal resistance and explore some potential ways that engineers might address this challenge in their design workflows.
To begin, we will briefly discuss what thermal resistance is and how it is measured.
What is Thermal Resistance?
The term ‘thermal resistance’ – also referred to as ‘R θ ’ – describes the rate of heat flow through a material (usually expressed in units such as degrees C per Watt or milliwatts per degree C).
For purposes of this discussion, we will define a thermally conductive paste as a measurement from the junction (the source of heat) to the ambient environment.
Recommender: 5 Things To Look Out For In Your Next Storage Water Heater
Understanding the problem of package thermal resistance begins!
Let’s understand the problem of package thermal resistance.
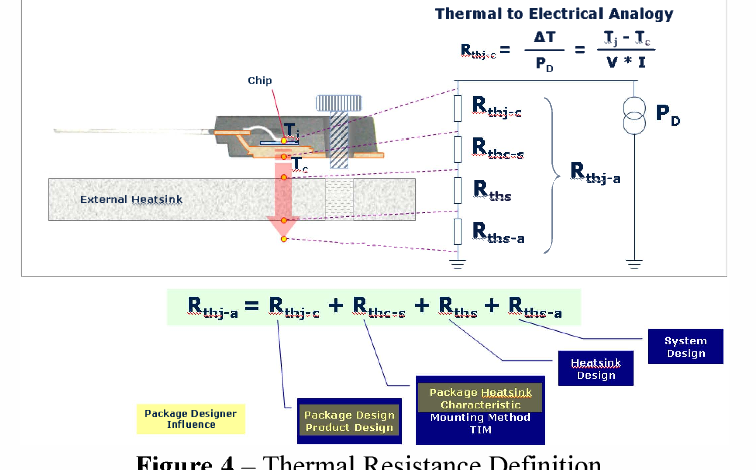
Imagine a heat source at the bottom of a package, which dissipates heat into an environment that is either free-flowing air or some other medium with which it can exchange thermal energy (such as oil).
From this point of view, we can model the radiating surface and ambient conditions in terms of their resistance to the surrounding atmosphere.
We can then use this model to measure different aspects of how effectively the package dissipates heat. For example, we might ask what is the total resistance of the complete system? Is it better for this number to be low or high? And…how does changing certain components of our model affect this result?
Looking at the model, we can say that thermal resistance (R θ ) is the quotient of the temperature difference across this interface and the heat flow (or power) at this interface.
Thermal Resistance = Temperature Difference/Heat Flow
To solve for either temperature difference or heat flow, there are two basic equations to use. The first is based on the heat flow (in Watts) and allows us to solve for the temperature differences. The second is based on the temperature difference (in °C) and allows us to solve for heat flow or power.
The total resistance of a system can be expressed by simply adding up all the individual resistances of each part in our model: R θ = R A + R B + … etc
Thermal Resistance = K/P
Where:
K = Thermal Conductivity (Watts / m.°C)
P = Heat Flow (Watts)
To solve for total thermal resistance, we can rearrange this equation to solve for P, or the heat flow.
R θ = K/P
P = K x R θ
We can also solve for the temperature difference by rearranging the first equation, where thermal resistance is defined as the quotient of the temperature difference and heat flow.
ΔT = P/Q
Where:
Q= P/K
Recommended: How do I remove super glue? Rules for removing from wood flooring
How to reduce package thermal resistance with a few simple steps
1. Lower the Junction Temperature
The first and most often quoted solution to lowering thermal resistance is to lower the operating temperature of our source (the junction).
We do not need to go into all the different ways in which we can accomplish this goal, but rather just look at how it affects our model, particularly in terms of the heat flow.
We see that lowering the temperature of our thermal source will reduce the heat flow at this interface, which reduces the overall thermal resistance.
2. Lower Thermal Resistance of Power Supply Path
The next step is to look for ways in which we can lower the resistance on paths leading to our source (the power supply).
The simplest way to do this is to choose the smallest possible resistance for each interface. As an example, power MOSFETs can be chosen based on their process geometry and thermal properties to minimize package Rθ.
3. Lower Thermal Resistance of Heat Dissipation Path
Next, we want to look at how well heat can carry away from our source.
To do this, we will solve for the thermal resistance of the heat dissipation path (R θ ).
Using Snell’s law and a simple model of parallel plates with convection at the interface, we can determine:
R θ = h / k A d T
Where:
h = convective heat transfer coefficient (Watts / m2.°C)
d T = Temperature Difference (ΔT)
k A = Thermal Conductivity of Air (Watts / m.°C)
The resistance defined by the following equation, where the second term represents the effect of geometry.
R θ = (d T / k A)(1/h)
As in the previous example, we can easily solve for ΔT by rearranging this equation. However, in this case, we will combine it with the second basic equation (the one where resistance defined as the quotient of the temperature difference and heat flow).